Unidad 2 Tecnología e incentivos
2.4 Empresas, tecnología y producción
- tecnología
- Descripción de un proceso que usa un conjunto de materiales y otros factores de producción, incluido el trabajo de personas y máquinas, para producir un producto.
Las empresas poseen o alquilan bienes de capital (por ejemplo, edificios y maquinaria) y emplean a trabajadores para producir y vender bienes y servicios. Una decisión importante que debe tomar cada empresa es la tecnología que elige para la producción: el proceso por el que convertirá una serie de factores (como materias primas y trabajo realizado por personas y por maquinaria) en un bien que pueda vender. Después de elegir una tecnología, también tendrá que decidir la cantidad de factores que utilizará, lo cual determinará cuánto podrá producir.
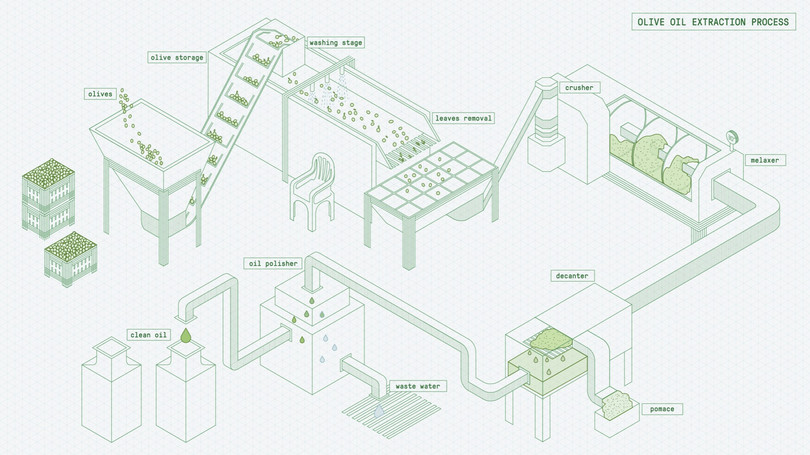
Por ejemplo, en la producción de aceite de oliva, hay que clasificar las aceitunas, lavarlas para quitar restos de tierra y piedras, molturarlas, separar pulpa y huesos, amasar la pulpa hasta hacer una pasta y prensar o centrifugar esta para extraer aceite y agua. Por último, el aceite se separa del agua y se envasa en latas o botellas. Durante miles de años, se ha producido usando técnicas simples en las que la mayor parte del proceso se llevaba a cabo de forma artesanal, con una mano de mortero para aplastar las aceitunas y piedras de molino para prensarlas. Los factores de producción eran materias primas (aceitunas y agua), capital (mortero y mano, piedras de molino) y trabajo. Era una tecnología que requería mucha mano de obra: para producir un litro de aceite, hacían falta unas 2000 aceitunas, además de muchas horas de duro trabajo.
- factor de producción
- Cualquier input que se introduce en un proceso de producción se denomina factor de producción. Los factores de producción pueden incluir maquinaria y equipos (normalmente denominados capital), mano de obra, tierra, energía y materias primas.
- función de producción
- Una función de la producción es una descripción gráfica o matemática de la relación existente entre la cantidad de factores de un proceso de producción y la cantidad obtenida del producto final.
La tecnología utilizada en una producción comercial moderna emplea menos mano de obra, más capital y más energía. Son factores de producción, también llamados inputs o insumos, las materias primas, el trabajo o mano de obra, los bienes de capital (máquinas para molturar, amasar y prensar) y la energía para hacer funcionar las máquinas.
Una tecnología puede representarse mediante una función de producción: relación que nos dice cuánta producción se obtendrá con una cantidad determinada de factores de producción. La tecnología descrita en la sección 1.6 genera productos agrícolas, Y, usando trabajo y tierra. Como la cantidad de tierra se supone constante, escribimos la función de producción como Y = f(X), donde X es el número de agricultores. Esta función se representa en la figura 1.8b.
En el caso del aceite de oliva, supón que N es el número de trabajadores empleados, M es el número de máquinas y E es la cantidad de energía utilizada por día. Podemos resumir la tecnología por medio de una función de producción de la cantidad de aceite de oliva obtenido por día, Y:
\[Y = \text{f}(M, N, E)\]
Esta expresión es una forma abreviada de decir que «la producción diaria de aceite, Y, depende (o es una función) de las cantidades de los factores N, M y E que la empresa decide utilizar». Hemos dejado de lado la materia prima, suponiendo que la cantidad de aceitunas que se necesita viene determinada automáticamente por el volumen de aceite que se va a producir.
La figura 2.3 describe una tecnología hipotética para elaborar aceite de oliva. Imagina que se necesitan tres máquinas (para molturar, amasar y prensar). Con la ayuda de un solo trabajador que las maneje y con 80 kWh de energía, pueden producir 50 litros de aceite de oliva al día. Si la empresa quiere producir más, necesita más máquinas, más trabajadores y más energía. La tabla muestra la producción conseguida con diferentes combinaciones de los factores de producción.
- tecnología de proporciones fijas
- Aquella tecnología que requiere factores en proporciones fijas entre sí. Para aumentar la producción, todos los factores deben incrementarse en el mismo porcentaje, de manera que mantengan las mismas proporciones entre sí.
- rendimientos constantes a escala
- Cuando la producción presenta rendimientos constantes a escala, aumentar todos los factores de producción en la misma proporción incrementa la cantidad producida en la misma proporción. La forma de la curva de costes medios a largo plazo de una empresa depende tanto de los rendimientos a escala en la producción como del efecto de la escala sobre los precios que paga por sus factores. Véase también: rendimientos crecientes a escala, rendimientos decrecientes a escala.
El que resulte sencillo describir esta tecnología se debe a dos motivos. El primero es que requiere factores de producción en proporciones fijas: por cada tres máquinas, se necesita un trabajador y 80 kWh de energía. Con una tecnología de proporciones fijas no tiene sentido incrementar uno de los factores de producción sin aumentar los demás. Por ejemplo, si tienes seis máquinas, no puedes hacer que funcionen más rápido aunque incorpores un tercer trabajador y añadas más energía: la producción seguirá siendo de 100 litros.
El segundo motivo es que tiene rendimientos constantes a escala: si duplicas los factores de producción, la producción resultante es el doble; de la misma manera, un aumento del 50 % en los factores de producción (la tercera fila de la tabla con respecto a la segunda) incrementa la producción en un 50 % (por lo que añadir más filas en la tabla no tiene complicación).
En la sección 2.5 usaremos tecnologías con estas dos propiedades para modelar las decisiones de las empresas en la Revolución Industrial.
Comparación de dos tecnologías
Supón que se ha desarrollado una nueva tecnología robótica para la elaboración del aceite de oliva. Para que funcione este sistema robotizado, basta con un trabajador y 400 kWh de energía y puede producir 100 litros de aceite de oliva al día. Como en el caso anterior, esta tecnología utiliza factores de producción en proporciones fijas y genera rendimientos constantes a escala. La producción diaria es proporcional al número de sistemas instalados. ¿Podemos decir que el sistema robotizado es mejor?
Una forma sencilla de comparar tecnologías con rendimientos constantes es confrontar los factores que necesitan para producir un cantidad determinada del producto final. La tabla de la figura 2.4 presenta los factores de producción que hacen falta para obtener 100 litros de aceite al día.
- producto medio
- El producto medio de un factor de producción es la producción total dividida entre la cantidad total del factor. Por ejemplo, el producto medio de un trabajador (también conocido como productividad del trabajo) es la producción total dividida entre el número de trabajadores empleados para producirla.
La cuarta columna se basa en estas cifras para comparar el producto medio del trabajo: producción por trabajador. Con proporciones fijas y rendimientos constantes, el producto medio del trabajo es el mismo, sea cual sea el número de trabajadores empleados. Por ejemplo, la producción por trabajador con la tecnología A es de 100/2 = 50 litros al día. La última columna muestra el cociente entre los dos factores y que la tecnología B consume más energía que la A.
La figura 2.4 refleja esa información de forma gráfica. En cada caso, muestra los factores necesarios para obtener 100 litros de aceite de oliva y, siguiendo la recta desde el origen, para otras cantidades de aceite. La pendiente de cada recta se corresponde con el cociente energía:trabajo. Cuanta más pendiente tenga la recta, más energía requiere esa tecnología (es decir, mayor es la cantidad de energía que requiere la obtención de un nivel dado de producto final en comparación con el número de trabajadores necesarios).
El gráfico muestra que ninguna tecnología es necesariamente mejor que la otra. El producto medio del trabajo es mayor con la tecnología B, pero usa mucha más energía. Para decidir cuál conviene utilizar, la empresa tendría que sopesar los costes relativos de los dos factores de producción. Ese fue un criterio clave al decidir la tecnología elegida en la Revolución Industrial, como se explica en las siguientes secciones de esta unidad.
Pregunta 2.5 Elige las respuestas que sean correctas
La figura 2.4 muestra los factores de producción necesarios para obtener diferentes cantidades de aceite de oliva usando dos tecnologías (A y B). Supón que existe una tercera tecnología de proporciones fijas, C, que requiere cuatro trabajadores y 360 unidades de energía para producir 100 litros de aceite de oliva. Teniendo en cuenta esta información, lee los siguientes enunciados y elige los que sean correctos.
- Producir 300 litros de aceite con la tecnología C necesitaría de 12 trabajadores y 1080 unidades de energía.
- El producto medio del trabajo de la tecnología C se encuentra entre el de A y el de B.
- El cociente energía:trabajo de la tecnología C se encuentra entre el de A y el de B.
- Los propietarios de la empresa preferirían la tecnología B a la C.
- Como C es una tecnología de proporciones fijas con rendimientos constantes a escala, multiplicamos las cifras dadas por 3 y, efectivamente, obtenemos 4 × 3 = 12 trabajadores y 360 × 3 = 1080 unidades de energía.
- El producto medio del trabajo de la tecnología C es de 100/4 = 25, que está por debajo del de A y B.
- El cociente energía:trabajo de la tecnología C es de 360:4 = 90, que se encuentra entre el de A (80) y el de B (400).
- La tecnología B tiene un producto medio del trabajo más alto que C, pero también consume más energía, por lo que la elección depende del precio relativo que tengan los factores de producción.
Ampliación 2.4 Funciones de producción
Esta ampliación explica cómo la tecnología de proporciones fijas empleada en la unidad 2 cubre las funciones de producción más típicas de las unidades 1 y 5.
En la segunda parte se exploran algunas propiedades matemáticas de las funciones de producción típicas, como las de las unidades 1 y 5, en concreto el producto medio decreciente del trabajo. Para esta parte, se necesitan conocimientos de análisis matemático (diferenciación).
La Introducción a las ampliaciones matemáticas explica brevemente lo que entendemos por análisis matemático y describe los conceptos que usamos, junto con su notación y convenciones.
La tecnología de proporciones fijas tratada en la parte principal de esta sección tiene utilidad para analizar algunos problemas; sin embargo, en la práctica suele ser posible variar la producción alterando un factor pero no otros. En el ejemplo de la tecnología agrícola tratado en la sección 1.6, se produce más grano cuando se aumenta el número de agricultores mientras se mantiene constante el otro factor, la tierra.
Supón que, en el caso del aceite de oliva, es posible modificar el número de trabajadores con respecto a los otros factores. Con una cantidad determinada de maquinaria y energía, la producción podría organizarse de una forma más o menos intensiva, dependiendo del número de trabajadores. De forma parecida, con una cantidad dada de mano de obra, aumentar el número de máquinas podría conllevar un aumento de la producción.
Para simplificar al máximo la descripción de la tecnología, suponemos que el capital (la maquinaria) y la energía se mantienen en proporciones fijas. Así que, sabiendo la cantidad de energía, también se conoce la cantidad de capital (maquinaria) que se utiliza. Por lo tanto, podemos pensar en la función de producción como una función de dos factores:
\[Y = f (N, E)\]
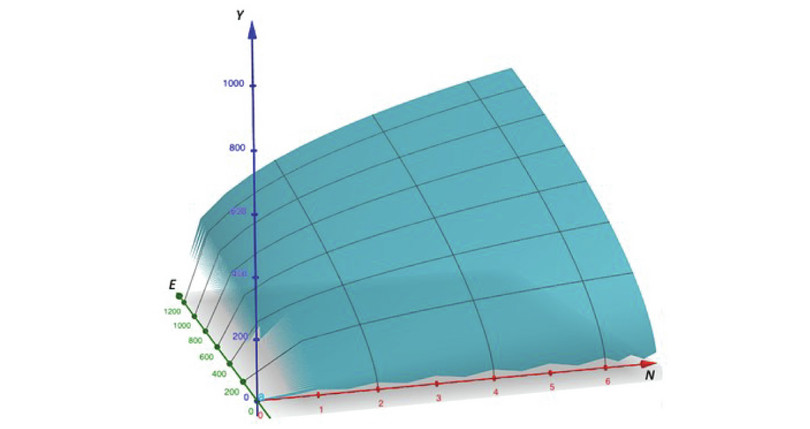
Los principales elementos que debe elegir la empresa son el número de trabajadores, N, y la cantidad de energía, E. Todo lo demás es consecuencia automática de lo elegido. Como ejemplo de función de producción similar a la descrita, la figura A2.1a muestra algunas combinaciones posibles de los factores, junto con la producción resultante.
Como en el ejemplo anterior, esta tecnología tiene rendimientos constantes a escala, tal como se constata observando las líneas A, C y F de la tabla. Pero, aunque añadiésemos más combinaciones, a partir de una tabla como esta no resultaría sencillo deducir cuál sería el efecto de variar un factor más que otro sobre la cantidad de aceite producido.
Es más fácil entender la relación si plasmamos la función de producción en un gráfico tridimensional como el de la figura A2.1b. El número de trabajadores, N, está representado en el eje x (rojo), y la cantidad de energía, E, en el eje y (verde). Estos dos ejes forman el «suelo» del gráfico y cada punto del suelo corresponde a una combinación diferente de N y E. Así, la correspondiente cantidad de aceite de oliva viene dada por la distancia que hay a la base, medida sobre el eje z (azul). Si trazamos la altura que corresponde a cada combinación (N, E), obtenemos una superficie suavizada, una «montaña» que se eleva conforme aumentan N y E. Sobre esa superficie aparecen marcados los puntos específicos incluidos en la tabla anterior.
Como sería de esperar, la imagen muestra que, cuanto más trabajo y más energía se utilizan, más aceite se produce. En segundo lugar, si se aumenta un factor mientras se mantiene constante el otro, la producción se incrementa, pero no tanto como cuando se aumentan los dos a la vez. Imagínate escalando la montaña desde el punto A, donde \(N = 2\) y \(E = 200\). Subir hasta el punto C (elevando los dos factores) supone un ascenso mucho más empinado que seguir la línea donde \(E = 200\).
Una función de producción con un solo factor variable
Es muy común que resulte más fácil variar unos factores que otros.
Por ejemplo, piensa en un pequeño productor de aceite de oliva que actualmente emplea a dos trabajadores y elabora 309 litros al día en el punto B de la figura A2.1c. Le gustaría ampliar la producción, porque el precio del aceite ha subido, pero no puede reunir el dinero para comprar más máquinas. Por lo tanto, la única forma que tiene de aumentar la producción es emplear a más trabajadores, sin que varíe el número de máquinas ni el correspondiente aporte de energía de 600. La línea de la figura A2.1c que pasa por los puntos B y F, la cual corresponde a \(E = 600\), muestra cómo variará la producción si se aumenta el personal. Si tomamos un corte vertical de la montaña siguiendo esa línea, tal como se muestra en el panel superior de la figura A2.1c, obtenemos un gráfico bidimensional (panel inferior).
El panel inferior muestra la producción de aceite de oliva como una función del trabajo únicamente, mientras que el otro factor, la energía, está fijo en 600. Esta función de producción presenta una forma curva (cóncava) parecida a la función de producción de la agricultura que vimos en la sección 1.6 (figura 1.8c). En ninguno de los dos casos sube la producción en proporción con el número de trabajadores, lo cual se debe a que existe un factor que no varía (la tierra en la unidad 1, la energía en esta sección). En la figura A2.1c, con una cantidad fija de energía y el capital correspondiente, al aumentar el número de trabajadores disminuye el número de máquinas por trabajador y, en consecuencia, la cantidad media que produce cada uno.
La función de producción y el producto medio decreciente del trabajo
En muchas aplicaciones económicas, se encuentran funciones de producción como la de la figura A2.1c, ya que normalmente es difícil alterar la cantidad de factores de producción como la tierra, los locales o la maquinaria. Por eso, necesitamos pensar en lo que sucedería si el trabajo variara mientras los demás factores se mantuvieran constantes. Lo habitual es que la producción aumente con más trabajo, pero los factores «fijos» limitan la productividad del trabajo y de ahí que baje la cantidad producida por trabajador.
En general, si \(x\) es el factor trabajo (podría expresarse como el número de trabajadores o como la cifra total de horas de trabajo) e \(y\) es la cantidad de producto obtenido (por ejemplo, litros de aceite de oliva), podemos escribir la función de producción de esta forma:
\[y = f(x)\]
\(f(x)\) podría ser cualquier tipo de función, pero si deseamos que represente una función de producción verosímil, debe tener ciertas propiedades. En primer lugar, si el factor trabajo es cero, no hay ninguna producción y, si es mayor que cero, la producción es estrictamente positiva:
\[f(0)=0, \quad f(x)>0 \text{ si } x>0\]
En segundo lugar, la función es creciente, es decir, cuando \(x\) aumenta, también lo hace \(y\). Por lo tanto, la pendiente de la función, que viene dada por su derivada, es positiva. Podemos escribir:
\[\frac{dy}{dx}>0\]
O lo que es lo mismo:
\[f'(x)>0\]
Si la función de producción tiene la típica forma cóncava del ejemplo del aceite de oliva, su pendiente \(f'(x)\) disminuye conforme \(x\) aumenta. Es decir, su segunda derivada es negativa:
\[f''(x)<0\]
La figura A2.1d muestra la pendiente decreciente, en la que hemos dibujado las tangentes en dos puntos, B y F, para comparar las pendientes de la función en ellos. La pendiente sigue siendo positiva, pero se hace más llana (menos positiva) hacia la derecha.
El producto medio del trabajo (PMT) viene dado por la producción total y dividida por el factor trabajo:
\[\text{PMT}=\frac{f(x)}{x}\]
Por ejemplo, en el punto B de la figura A2.1d, la empresa emplea a dos trabajadores y produce 309 litros de aceite al día. El producto medio del trabajo en B corresponde a la pendiente de la línea desde el origen hasta el punto B:
\[\begin{align*}
\text{producto medio del trabajo} &= \frac{\text{producción total}}{\text{número total de trabajadores}} \\
&= \frac{309~ \text{litros}}{2~ \text{trabajadores}} \\
&= 155~ \text{litros por trabajador}
\end{align*}\]
- producto medio decreciente del trabajo
- Propiedad de un proceso de producción en el que, a medida que aumenta el factor de trabajo, disminuye la cantidad producida por unidad de trabajo (el producto medio).
El ejemplo del aceite de oliva, como todas las funciones de producción que tienen esta forma cóncava típica, presenta la propiedad del producto medio decreciente del trabajo. Cuanto más avanzamos por la línea, más llana se hace la función de producción y más cae el producto medio del trabajo: en F, la productividad media del trabajo ha caído a 480/6 = 80 litros por trabajador.
Hemos descrito la función de producción por medio de dos pendientes diferentes: la pendiente de la función, \(f'(x)\), y la de la recta que sale del origen, \(\text{PMT}=f(x)/x\).
Podemos demostrar que, si una función de producción tiene la propiedad del producto medio decreciente, su pendiente \(f'(x)\) siempre debe ser más baja que el producto medio del trabajo. Derivando el producto medio con respecto a \(x\) mediante la regla del cociente, obtenemos:
\[\frac{d\text{PMT}}{dx} = \frac{d}{dx}\left(\frac{f(x)}{x}\right) = \left(\frac{xf'(x)-f(x)}{x^2}\right)\]
Si el producto medio es decreciente, esta expresión debe ser negativa:
\[\begin{align*}
\frac{d\text{PMT}}{dx} < 0 \Rightarrow xf'(x)-f(x) < 0
\end{align*}\]
\[\begin{align*}
\Rightarrow f'(x) < \frac{f(x)}{x}
\end{align*}\]
La pendiente de la función de producción se denomina producto marginal del trabajo y desempeña un papel importante en los modelos económicos. La estudiamos en detalle en las ampliaciones de la unidad 5.
Es decir, la pendiente de la función de producción es más baja que el producto medio del trabajo.
Ejercicio A2.1 Dibujo de funciones de producción
Otra empresa que produce aceite de oliva tiene la función de producción \(Y = 0,5E^{0{,}8}N^{0{,}4}\), donde \(E\) es la cantidad de energía utilizada y \(N\) es el número de trabajadores empleados. Supón que la cantidad de energía es constante en 100 unidades.
- Dibuja la función de producción para \(N\) = 0 hasta \(N\) = 100, con la producción (\(Y\)) en el eje vertical y el número de trabajadores (\(N\)) en el horizontal.
- Halla el producto marginal del trabajo (usando análisis matemático) y el producto medio del trabajo cuando el número de trabajadores es 10, 50 y 100, y confirma si ambos son decrecientes. Explica este resultado haciendo referencia a las propiedades matemáticas de la función de producción.
- ¿También disminuyen con la energía tanto el producto medio como el marginal? Explica por qué sí o por qué no.
Más información: sección 7.3 (en especial, la página 127) y sección 8.2 de Malcolm Pemberton y Nicholas Rau, Mathematics for Economists: An Introductory Textbook (4th ed., 2015 o 5th ed., 2023). Manchester: Manchester University Press.