第2单元 技术与激励
2.4 企业、技术和生产
- 技术（technology）
- 这是对一个生产过程的描述，该过程利用一系列原材料和其他投入（包括人力和机器的劳动）来进行生产。
企业拥有或租赁资本货物（如厂房和设备），并雇佣工人来生产和销售商品与服务。企业面临的一个关键决策是选择生产技术，即如何将一组投入（如原材料以及人力和机器的作用）转化为可供销售的产品。在选定技术后，企业还需确定各类投入品的使用量，这将决定其能够生产的产出量。
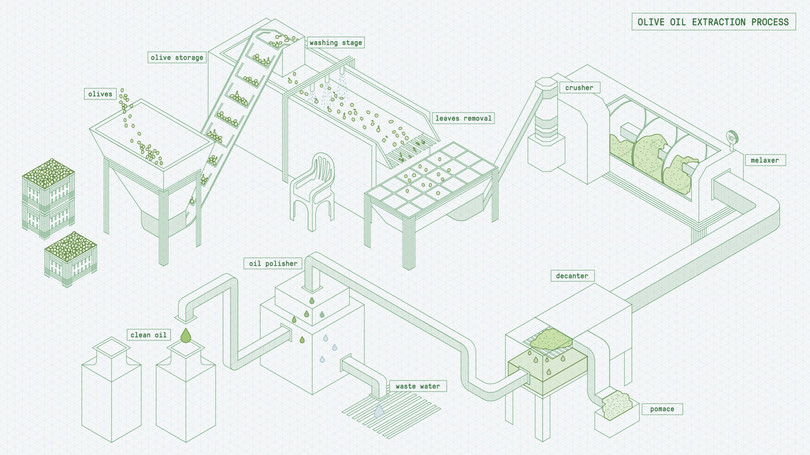
例如，在橄榄油的生产过程中，橄榄需要经过分拣、清洗、研磨去核、捣碎成糊、压榨提取油水混合物等工序。最终，将橄榄油从水中分离，并进行罐装或瓶装。数千年来，橄榄油生产一直沿用简单工艺，大部分工序依赖人力操作，例如人们用杵臼捣碎橄榄，再用重石压榨。这一过程的要素投入包含原材料（橄榄和水）、资本（杵臼和石块）以及劳动力。这是一种劳动密集型技术：每生产1升橄榄油需投入2000颗橄榄与数小时高强度劳动。
用于生产橄榄油的劳动密集型技术。
用于生产橄榄油的资本密集型技术。
- 生产要素（factors of production）
- 任何用于生产过程的投入品都被称为生产要素。生产要素包括劳动、机器和设备（通常称为资本）、土地、能源和原材料等多种类型。
- 生产函数（production function）
- 生产函数以图形或数学形式描述了生产过程中投入要素数量与产出数量之间的关系。
现代商业化生产所采用的技术减少了对劳动力的依赖，而增加了对资本与能源的使用。投入品（即生产要素）包括原材料、劳动力、资本品（如研磨机、捣碎机与压榨机）以及用于驱动机器的能源。
技术可以用生产函数表示：给定使用的投入品数量，该函数关系可确定与之对应的产出水平。以1.6节中介绍的技术为例，该技术使用劳动力与土地生产农产品(\(Y\))。由于假定土地数量固定不变，其生产函数可记为\(Y\) = f(\(X\))，其中\(X\)表示参与劳动的农民数量。该函数的形态可见图1.8b。
在橄榄油的例子中，设\(N\)为雇佣的工人数量，\(M\)为机器数量，\(E\)为每日能源消耗量。我们可以将技术表示为橄榄油每日产量(\(Y\))的生产函数：
\[Y = \text{f}(M, N, E)\]这一表达式简洁地表示了“橄榄油每日产量\(Y\)取决于企业选用的投入品数量\(N\)、\(M\)和\(E\)（或者说是投入品数量的函数）”。我们在此忽略了原材料投入，假定生产所需橄榄数量由目标产油量自动确定。
假设存在一种如图2.3所示的橄榄油生产技术。生产设备包含3台机器（分别用于研磨、捣碎和压榨）。该套设备需配备一名操作工人，每日消耗80千瓦时能源，可以生产出50升橄榄油。如果企业想要扩大产能，则需增加机器、工人和能源投入。表格展示了在这一技术下不同生产要素组合对应的产出水平。
| 机器数量，\(M\) | 工人数量，\(N\) | 能源用量， \(E\) （千瓦时） | 产量，\(Y\)（升） |
|---|---|---|---|
| 3 | 1 | 80 | 50 |
| 6 | 2 | 160 | 100 |
| 9 | 3 | 240 | 150 |
| 12 | 4 | 320 | 200 |
图2.3 以固定比例技术生产橄榄油的情形
- 固定比例技术（fixed-proportions technology）
- 一种要求各投入要素以固定比例组合的技术。如需提高产量，所有投入要素须以相同比例增加，以维持彼此间的固定比例关系。
- 规模报酬不变（constant returns to scale）
- 当生产活动呈现规模报酬不变的特征时，将生产过程中的所有投入要素按相同比例增加，产出也会按相同比例增加。企业的长期平均成本曲线形状既取决于生产过程中的规模报酬特征，也取决于规模变化对其投入要素价格的影响。 参见：规模报酬递增，规模报酬递减.
这种技术易于描述，主要基于两个原因。首先，它要求投入要素以固定比例组合——每3台机器需配备一名工人和80千瓦时能源。在固定比例技术下，单独增加某一种投入不会产生任何效果。例如，假设你此时拥有6台机器，即便你将工人数量增至3人或者供应更多的能源，也无法提升设备运行速度，产量仍将维持在100升的水平上。
其次，该技术具备规模报酬不变的特性：投入翻倍则产出翻倍；同理，投入量增加50%（如表内第二行至第三行），产出也会提升50%（因此，你可以很容易地扩充表格数据）。
在2.5节，我们将使用这两项技术特性，构建工业革命时期的企业决策模型。
比较两种技术
假设开发出一种新型机器人技术用于橄榄油生产。该机器人系统由一名工人操控，每日消耗400千瓦时能源，可以生产100升橄榄油。与原有技术一样，该技术也具有固定比例投入和规模报酬不变的特征。每日产量与系统安装数量成正比。我们能否认为机器人系统更具优势呢？
对于规模报酬不变的技术，一种简单的比较方法是比较它们生产相同产出所需的投入量。图2.4中的表格展示了每日生产100升橄榄油所需的各类投入数量。
- 平均产量（average product）
- 生产要素的平均产量指的是总产量与该生产要素总投入量的比值。例如，工人的平均产量（也称为劳动生产率）是总产量除以参与生产的工人人数。
第四列基于上述数据比较了两种技术的劳动平均产量，即工人的人均产量。在固定比例和规模报酬不变的技术特征下，无论雇佣多少工人，劳动的平均产量始终保持不变。例如，技术A的工人的人均产量为100/2=50升/天。最后一列展示了两种投入要素使用量的比值：它表明技术B比技术A更加能源密集。
| 生产100升橄榄油的要素需求量 | ||||
|---|---|---|---|---|
| 工人数量 | 能源使用量 | 平均劳动产量 | 能源—劳动比率 | |
| A：研磨机、捣碎机和压榨机 | 2 | 160 | 50 | 80 |
| B：机器人技术 | 1 | 400 | 100 | 400 |
图2.4 总结和比较两种固定比例技术。
图2.4的下半部分以图形方式对两种技术进行比较。它展示了两种技术情形下生产100升橄榄油和更高产量（沿着从原点出发的射线向右上方延伸）所需的要素投入量。每根射线的斜率对应着该技术的能源—劳动力比率。射线越陡峭，技术的能源密集度越高（单位产出所需能源相对于劳动力更多）。
图2.4表明，两种技术不存在绝对优劣之分。虽然技术B的劳动平均产量更高，但其能源使用量也远高于技术A。企业的技术选择需要基于两种要素的相对价格进行权衡。正如本单元后续内容所述，这正是工业革命时期影响企业技术选择的关键因素。
问题2.5 选择正确答案（多选题）
图2.4展示了使用两种技术（A和B）生产不同数量橄榄油对投入品的需求。假设存在第三种固定比例技术C，该技术生产100升橄榄油需要4名工人和360单位能源。根据上述信息，阅读以下陈述并选择正确选项：
- 由于技术C是固定比例且规模报酬不变的技术，我们可将给定数值乘以3（4×3=12名工人，360×3=1,080单位能源）得出相应的投入要素需求。
- 技术C的劳动平均产量为100/4=25，低于技术A和技术B的劳动平均产量。
- 技术C的能源—劳动比率为360/4 = 90，介于技术A（80）和技术B（400）之间。
- 技术B虽较技术C具有更高的劳动平均产量，但能源密集度更高，因此企业主的选择将取决于投入要素的相对价格。
扩展2.4 生产函数
本扩展部分将阐述第2单元中使用的固定比例技术与第1单元和第5单元中更为典型的生产函数之间的关系。
第二部分探讨了典型生产函数（例如第1单元和第5单元中出现的那些生产函数）的一些数学性质，特别是劳动平均产量递减的性质。理解这一部分内容需要掌握微积分（求导）的知识。
《数学拓展导论》简要介绍了我们所说的微积分的含义，并说明了理解本部分内容所需的数学水平、符号和惯例。
本节核心部分所讨论的固定比例技术在分析某些问题时非常方便，但在实际生产活动中，人们往往可以通过仅改变一种要素的投入量来调整产量水平，而无需同时调整其他要素的投入量。例如，在1.6节关于农业技术的示例中，当农民数量增加而另一要素（土地）保持不变时，产量也会增加。
假设在橄榄油生产过程中，工人相对其他投入要素的使用数量可以发生变化。在给定机器和能源使用数量的情况下，企业可通过增减工人数量实现更为集约或更为宽松的生产模式。类似地，给定劳动力数量，增加机器数量也可能带来产量提升。
为尽可能简化对技术的描述，我们假定资本（机器）与能源保持固定比例。一旦确定了能源用量，资本（机器）的投入量也随之确定。此时，生产函数可以表示为以下两个投入要素的函数：
\[Y = f (N, E)\]企业的核心决策变量是工人数量（\(N\)）和能源使用量（\(E\)），其余要素将根据这两个变量自动调整。图E2.1a展示了在这种生产函数下，一些投入要素组合与对应产量的示例。
| 工人数量，N | 能源使用量，E（千瓦时） | 产量，Y（升） | |
|---|---|---|---|
| A | 2 | 200 | 160 |
| B | 2 | 600 | 309 |
| C | 4 | 400 | 320 |
| D | 4 | 800 | 485 |
| F | 6 | 600 | 480 |
| G | 6 | 1000 | 652 |
图E2.1a 一种可变比例技术：工人数量（\(N\)）、能源使用量（\(E\)）的若干组合以及对应产量（\(Y\)）。
与之前的例子类似，该技术仍具有规模报酬不变的特性——通过比较表中的行A、C和F即可验证。然而，即便罗列更多投入要素组合，我们仍难以从类似表格中直观判断某一要素使用量相对其他要素增加会对橄榄油产量形成何种影响。
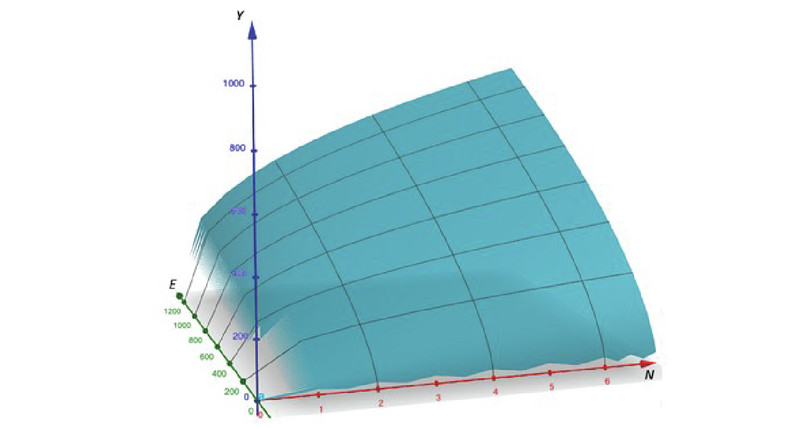
我们可以利用如图E2.1b所示的三维图形更清晰地呈现生产函数的特性。在该图中，x轴（红色）表示工人数量（\(N\)），y轴（绿色）表示能源使用量（\(E\)），二者共同构成图形的“底面”，底面上的每一点均对应不同的\(N\)-\(E\)组合。相应的产油量则表示为距离底面的高度，即z轴（蓝色）的取值。若将所有\(N\)-\(E\)组合对应的高度在坐标系中标记出来，将形成一个平滑的曲面——一座随着\(N\)和\(E\)的增加而抬升的“山丘”。表中所包含的各要素组合点均已标记于该曲面之上。
图E2.1b 橄榄油生产函数的三维图示：\(Y = f(N, E)\)。
该图表明：首先，随着劳动和能源投入量的增加，产油量也随之提高，这符合我们的预期。其次，若保持某一要素使用量不变，仅增加另一要素使用量，产量虽会有所上升，但其增速不及两种要素使用量同时增加的情形。试想从A点（\(N\)=2，\(E\)=200）出发，沿着该曲面攀爬：若同时提升两种要素投入以前往C点（\(N\)=4，\(E\)=400），其攀爬路径的坡度将远比沿着\(E\)=200线即仅增加劳动投入时爬升的坡度要陡。
存在一种可变要素的生产函数
在实际生产过程中，调整某些要素的使用量通常比调整其他要素更为容易。
例如，假设某小型橄榄油生产商目前雇佣了2名工人，日产量为309升（对应图E2.1c的B点）。由于橄榄油价格上涨，企业急需扩大产能，但因融资困难无法购置新机器。因此，企业提升产能的唯一途径是在保持当前机械设备存量和对应能源投入（600单位）不变的情况下，增加雇佣工人的数量。图E2.1c中穿过点B（\(N\)=2，\(E\)=600）和点F（\(N\)=6，\(E\)=600）的连线（对应\(E\)=600）展示了劳动力增加对产出的影响效应。沿着这条连线对“山丘”进行垂直切片（图E2.1c的上半部分），可以得到生产函数的二维图示（图E2.1c的下半部分）。
图E2.1c 能源使用量保持不变时橄榄油的生产函数。
图E2.1c的下半部分展示了在能源使用量固定为600单位时，橄榄油产量仅是劳动力数量的函数。该生产函数呈现出类似1.6节中农业生产函数（图1.8c）的曲线形态（凹形）。在这两个案例中，产出都不会随劳动者数量成比例上升，这是因为存在一个固定要素（第1单元中的土地与这里的能源）。在图E2.1c中，当能源使用量和对应的资本数量固定不变时，人均机器数量会随着劳动力数量的增加而减少，从而导致人均产量同步下降。
生产函数与劳动平均产量递减
你可能会在许多经济学应用场景中遇到如图E2.1c所示的生产函数。由于土地、厂房或机器等要素往往难以在短时间内调整投入数量，因此我们通常会重点关注在其他要素保持固定的情况下，劳动投入变化所带来的影响。通常而言，增加劳动力投入数量可以提升总产量，但由于“固定”投入限制了劳动生产率，因此工人的平均产量会降低。
总的来说，假如设劳动力投入量为\(x\)（可以使用工人数量或他们的总工时来衡量），产出量为\(y\)（例如，橄榄油的升数），则生产函数可以表示为：
\[y = f(x)\]生产函数\(f(x)\)可采用任意函数形式，但如果想使其符合现实经济特征，则须满足以下性质：首先，如果投入为零，则产出为零，如果投入大于零，则产出严格为正：
\[f(0)=0, \quad f(x)>0 \text{ 如果 } x>0\]其次，函数具有单调递增性：即随着\(x\)增加，\(y\)也相应提高，因此函数曲线的斜率（其导数值）始终为正：
\[\frac{dy}{dx}>0\]或等价地：
\[f'(x)>0\]若生产函数呈现出典型的凹形形态（如橄榄油的例子所示），则其斜率\(f'(x)\)随\(x\)增加而递减，即二阶导数为负：
\[f''(x)<0\]图E2.1d通过对比B点和F点处的切线斜率，直观呈现了这一斜率递减的特征。此时生产函数的斜率依然为正，但随着函数上的点向右移动，曲线逐渐变得平坦——斜率的数值变小了。
劳动平均产量 (APL) 可以由总产出\(y\)除以劳动投入\(x\)得到：
\[\text{APL}=\frac{f(x)}{x}\]
图E2.1d 生产函数的斜率和劳动平均产量。
以图E2.1d中的B点为例，此时企业雇佣了2名工人，每天生产309升橄榄油。B点的APL对应于从原点至B点连线的斜率：
\[\begin{align*} \text{劳动平均产量} &= \frac{\text{总产出}}{\text{工人总数}} \\ &= \frac{309~ \text{升}}{2~ \text{名工人}} \\ &= 155~ \text{升/工人} \end{align*}\]- 劳动平均产量递减（diminishing average product of labour）
- 指生产过程中随着劳动投入增加，单位劳动产出（平均产量）逐渐下降的特性。
与所有具有典型凹形形态的生产函数一样，在橄榄油的例子中，生产函数呈现出劳动平均产量递减的特性：随着劳动投入增加，生产函数曲线逐渐变得平坦，APL随之下降；在F点处，劳动平均生产率已降至480/6=80升/工人。
我们已经使用了两种不同的斜率来描述生产函数：一个是生产函数本身的斜率\(f'(x)\)，另一个是从原点引出射线的斜率\((\text{APL}=f(x)/x)\)。
我们将证明，若某生产函数具有平均产量递减的特性，则其斜率\(f'(x)\)必定始终小于APL。对APL关于\(x\)求导（应用商的求导法则），可得：
\[\frac{d\text{APL}}{dx} = \frac{d}{dx}\left(\frac{f(x)}{x}\right) = \left(\frac{xf'(x)-f(x)}{x^2}\right)\]如果平均产量递减，则该导数必为负值：
\[\begin{align*} \frac{d\text{APL}}{dx} < 0 \Rightarrow xf'(x)-f(x) < 0 \end{align*}\] \[\begin{align*} \Rightarrow f'(x) < \frac{f(x)}{x} \end{align*}\]生产函数的斜率被称为劳动边际产量。边际产量是经济学模型的核心概念，我们将在第5单元的扩展部分对其展开深入探讨。
也就是说，生产函数的斜率小于APL。
习题E2.1 绘制生产函数
某橄榄油企业的生产函数为\(Y = 0.5E^{0.8}N^{0.4}\)，其中\(E\)为能源使用量，\(N\)为工人数量。假设能源使用量固定为100单位。
- 请绘制当\(N\)从0到100时的生产函数曲线，其中纵轴表示产出(\(Y\))，横轴表示工人数量(\(N\))。
- 使用微积分方法计算工人数量分别为10、50和100时的劳动边际产量与平均产量。验证二者是否呈现递减趋势，并结合生产函数的数学性质解释这一结果。
- 能源使用量是否也存在平均产量与边际产量递减的特性？请说明判断依据。
延伸阅读：马尔科姆·彭伯顿（Malcolm Pemberton）和尼古拉斯·劳（Nicholas Rau）的《经济学家需要掌握的数学：一本入门教材》7.3节（特别是第127页）和8.2节。Malcolm Pemberton and Nicholas Rau. Mathematics for Economists: An Introductory Textbook (4th ed., 2015 or 5th ed., 2023). Manchester: Manchester University Press.
